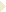Dziennik elektroniczny     Facebook    Start    Kontakt   

Strona o programowaniu w języku LOGO

Fraktale

Definicja

Fraktal Fraktal (łac. fractus – złamany, cząstkowy, ułamkowy) w znaczeniu potocznym oznacza zwykle obiekt samo-podobny (tzn. taki, którego części są podobne do całości).
Fraktal ma względnie prostą definicję rekurencyjną.

Trójkąt Sierpińskiego

Jeden z najprostszych fraktali.
Konstrukcja tego zbioru była podana przez polskiego matematyka Wacława Sierpińskiego w 1915.

Trójkąt Sierpińskiego otrzymuje się następująco: w trójkącie równobocznym łączy się środki boków, dzieląc go w ten sposób na cztery mniejsze trójkąty. Trójkąt środkowy usuwa się, a wobec trzech pozostałych trójkątów operację się powtarza, dzieląc każdy z nich na cztery mniejsze trójkąty, usuwając środkowy, a wobec pozostałych czynności się powtarzają. Punkty pozostające po nieskończenie wielu powtórzeniach tej operacji tworzą trójkąt Sierpińskiego.

---

Źródło:
http://pl.wikipedia.org/wiki/Tr%C3%B3jk%C4%85t_Sierpi%C5%84skiego

---

Dywan Sierpińskiego

Dywan Sierpińskiego to fraktal otrzymany z kwadratu za pomocą podzielenia go na dziewięć (3x3) mniejszych kwadratów, usunięcia środkowego kwadratu i ponownego rekurencyjnego zastosowania tej samej procedury do każdego z pozostałych ośmiu kwadratów.

Procedura wywołana z parametrem :n wynoszącym 4

Dywan Sierpińskiego


Jeśli powyżej nie jest widoczna zawartość projektu, to należy zainstalować wtyczkę. Niestety nie działa ona prawidłowo z wersjami 64-bitowymi przeglądarek internetowych.
Jednak możesz zainstalować na swoim komputerze 32-bitową wersję przeglądarki Opera
i za jej pomocą oglądać udostępniane projekty.

Płatek Kocha

Krzywa Kocha powstaje z odcinka, poprzez podzielenie go na 3 części i zastąpienie środkowej ząbkiem (o ramieniu długości równej 1/3 odcinka) takim, że wraz z usuwaną częścią tworzy trójkąt równoboczny. Krok ten jest powtarzany w nieskończoność dla każdego fragmentu odcinka.

Krok 0
Krzywa Kocha w kroku zerowym (k=0) jest odcinkiem. Zostanie on podzielony na 3 równe części, a środkową zastąpią dwa odcinki długości 1/3 l, nachylone względem niej pod kątem 60°. Wraz z wyciętym fragmentem mogłyby one utworzyć trójkąt równoboczny.

Krok 1
Krzywa Kocha w kroku pierwszym (k=1), po transformacji zawiera 4 odcinki, każdy równy 1/3 l. W kolejnym kroku każdy z tych odcinków ponownie zostanie podzielona 3 części, a środkową znów zastąpimy dwoma odcinkami.

Krok 2
Krzywa Kocha w kroku drugim (k=2) zawiera już 16 odcinków, każdy długości 1/9 l. W kolejnym kroku (k=3) powstanie 64 odcinków, każdy długości 1/27 l itd.

Kolejne wywołania koch ze stopniami odpowiednio: 0 1 2 3 4.

Procedura tworząca krzywą Kocha wygląda następująco:

Połączenie trzech krzywych przypomina płatek śniegu i nazywane jest płatkiem Kocha (na rysunku poniżej).

Płatki śniegu


Jeśli powyżej nie jest widoczna zawartość projektu, to należy zainstalować wtyczkę. Niestety nie działa ona prawidłowo z wersjami 64-bitowymi przeglądarek internetowych.
Jednak możesz zainstalować na swoim komputerze 32-bitową wersję przeglądarki Opera
i za jej pomocą oglądać udostępniane projekty.

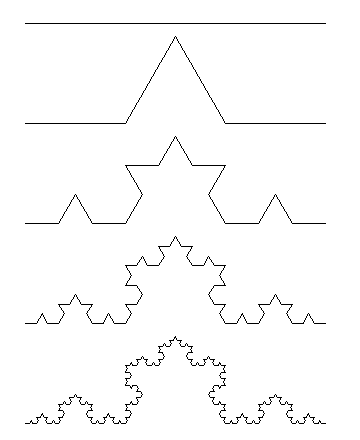
Plaster miodu

krok 0
rysujesz sześcian

krok 1
rysujesz sześć mniejszych sześcianów na początku każdego boku

krok 2
rysujesz sześcian na boku każdego z małych sześcianów

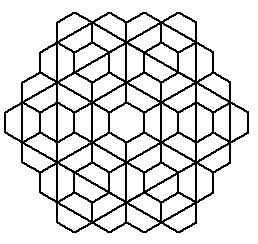
Drzewa binarne

Binarne oznacza dwójkowe, nazwano je tak gdyż z każdego rozgałęzienia wyrastają dwie podobne gałęzie.
Drzewo binarne charakteryzuje jego stopień - liczba poziomów oraz wielkość. Popatrzmy na drzewo stopnia 3.

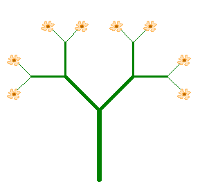
Pień - to drzewo stopnia 1, z niego wyrastają dwie gałęzie - obie to drzewa stopnia 2. Gałęzie te wyrastają pod kątem 45 stopni i obie mają długość równą 0.7 długości pnia. Podzielmy konstrukcję drzewa na elementy podstawowe i drzewa niższego stopnia. Elementem podstawowym jest pień o pewnej długości, dalej mamy identyczne dwa drzewa niższego stopnia i o wielkości 0.7 mniejszej niż drzewo pierwotne. Jedno z drzew niższego stopnia jest odchylone od pnia w lewo o 45 stopni. Drugie z nich zaś jest odchylone o 90 stopni w prawo od pierwszego.
Spróbujmy zapisać plan procedury DRZEWO z parametrami nazwa żółwia stopień i wielkość:

przejście naprzód o wielkość pnia
sprawdzenie warunku: czy stopień wynosi 0
jeśli tak, to zakończenie procedury
jeśli nie, to:
skręt w lewo o 45 stopni
utworzenie nowego żółwia o kierunku w prawo 90 w stosunku do kierunku wyjściowego (lewo 45)
wywołanie procedury DRZEWO z parametrami stopień-1 i wielkość*0.7)


Nazwa żółwia ustalana jest poprzez parametr :lż od 0 aż do np. 64 przy atrybucie :n wynoszącym 6
Numer żółwia w nazwie zwiększa się za każdym razem o 1 dzięki funkcji długość kto  – w wyniku wywołania której za każdym razem otrzymujemy aktualną liczbę zółwi na stronie.

Drzewko


Jeśli powyżej nie jest widoczna zawartość projektu, to należy zainstalować wtyczkę. Niestety nie działa ona prawidłowo z wersjami 64-bitowymi przeglądarek internetowych.
Jednak możesz zainstalować na swoim komputerze 32-bitową wersję przeglądarki Opera
i za jej pomocą oglądać udostępniane projekty.

Liść paproci

Na koniec ciekawy motyw roślinny.
Fraktale naprawdę są wśród nas.

Procedura rysowania liścia paproci pokazanego po prawej.

Wywołanie np.:

SPONSORZY

ING BAnk Śląski SA
Oddział w Katowicach
5 komputerów polizingowych 2008

---

MEN oraz Europejski Fundusz Społeczny Projekt „Pracownie komputerowe dla szkół” rok 2005

---

Urząd Miasta Łziska Górne
Pracownia 10 komputerów rok 2002